In periodic time series it’s possible make an aproximation of them using discrete fourier transform given by the following equation:

Also it’s possible express them using sin functions only:

Then we can express this model for example on pytorch to find the parameters $A_{k}$, $B_{k}$ for the first model or $A_{k}$, $P_{k}$ for the last model.

In my particular problem the tiemeseries has two seasonings daily and weekly and timeseries buckets are 10 minutes long, then $N$ has to be the amount of buckets of 10 minutes in one week.

One interesting thing is that if applying box-cox transformation it makes the learning faster.

The box-cox transformation is given by the following equation:

When $\lambda = 0$ then box-cox transformation is like $\log$ function. $\lambda$ must take values between 0 and 1.

The box-cox transformation maintains the anomalies and reduce the magnitude of the noise, because reduce the scale of timeseries. When using the transformed timeseries the function to learn in simpler than the original.

The tricky part to detect anomalies is make the learned function smoother. We can acomplish that not taking into account the high frequencies in the fourier model. Doing in that way the learned function has less noise, then is more easy to detect anomalies in the original timeseries. Filter frequencies has another benefit for learning, the amount of features decrease, then the learning is faster.

Pytorch implementation

import torch
import numpy as np
import pandas as pd
import seaborn as sbn
import matplotlib.pyplot as plt
from scipy.stats import boxcox
from torch import optim
import  torch.nn.functional as F

x_train = torch.tensor(x_ts_train, dtype = torch.float32, requires_grad=False)
y_train = torch.tensor(y_ts_train,dtype = torch.float32, requires_grad=False)

class FourierModel(torch.nn.Module):
    def __init__(self):
        super(FourierModel, self).__init__()
        self.multipliers = torch.tensor([(x*2*PI)/PERIOD for x in range(THRESHOLD,PERIOD)], requires_grad=False)
        self.amplitudes_cos = torch.rand(1, PERIOD - THRESHOLD, requires_grad=True)
        self.amplitudes_sin = torch.rand(1, PERIOD - THRESHOLD, requires_grad= True)
        self.bias = torch.zeros(1, requires_grad=True)
        
    def parameters(self):
        return [self.amplitudes_sin, self.amplitudes_cos, self.bias]
        
    def forward(self, x):
        sin_part = torch.sum(torch.sin(x.view(-1, 1) * self.multipliers) * self.amplitudes_sin, dim=1)
        cos_part = torch.sum(torch.cos(x.view(-1, 1) * self.multipliers) * self.amplitudes_cos, dim=1)
        return sin_part + cos_part + self.bias

model = FourierModel()
optimizer = optim.Adam(model.parameters(), lr=0.5)
epochs = 400

for i in range(epochs):
    optimizer.zero_grad()
    y_pred = model.forward(x_train)
    loss = F.mse_loss(y_train, y_pred)
    loss.backward()
    optimizer.step()

Plot timeseries transformed, learned function and anomalies

To detect anomalies I calculated the noise (difference between timeseries and learned function), then calculate noise standard deviation and calculate the point where the noice obsolute value is greater that 3 times std. The blue line is the learned function, the red one is the transformed timeseries and the green point are the anomalies.

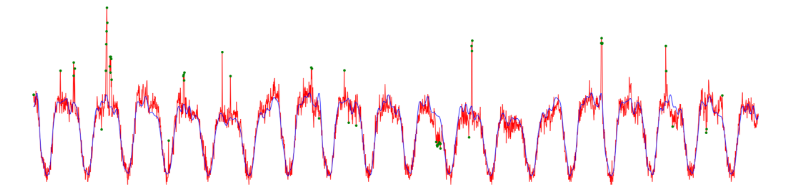
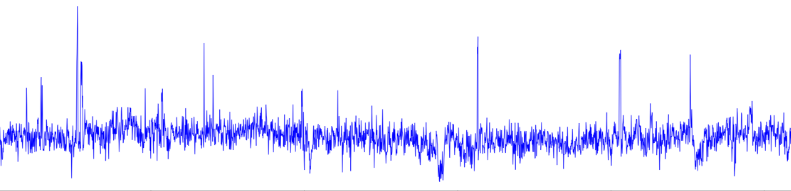
The noise

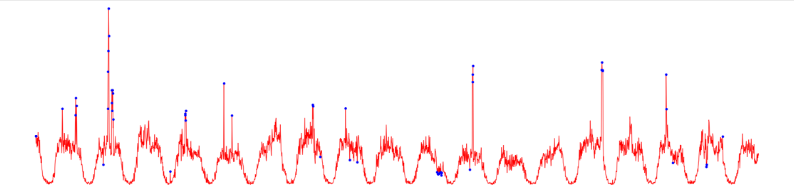
Plot anomalies in the original tiemseries

Here is the plot of the previous anomalies on the original timeseries

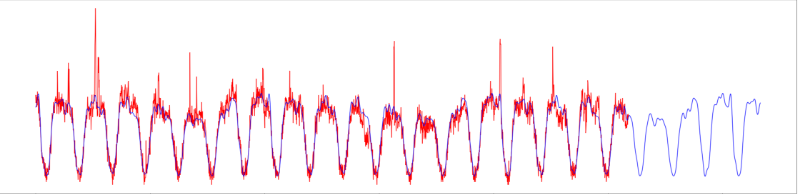
Forecasting

After learn parameters of fourier model it’s possible evaluate on futures points in time.

Code

You can find the code in this Notebook